Stability selection

Stability selection: differences in models due to different data sets

Suppose we have collection of regression models \(M_1, M_2, \ldots, M_p\). By a regression model we here mean a set of predictors and a model for the response. To asses the predictive ability of the models we perform cross validation: Fit each model to one set of data and predict another set of data, do so repeatedly. Compute a prediction error for each model. The model with the smallest prediction error is the best model.

But before we get there, we need to select a model to generate the collection of candidate models. One approach is the following:

A model selection method consists of two parts:

A criterion for selecting a model and
A strategy for generating candidate models, that is a strategy for navigating the model space.

If we have \(K\) datasets we can perform \(K\) model selections, and this gives us a collection of candidate models. We can then perform cross validation on these models. Say we want to perform \(K\) different model selections. We can do this by resampling or by creating subgroups. Resampling is done by drawing \(n\) observations with replacement from the data set. Subgroups are created by dividing the data set into \(K\) subgroups as follows: Form \(K\) subgroups by dividing the data set into \(K\) equal parts. Then for each \(k=1,\ldots,K\) the \(k\)th subgroup is left out and the model is fitted to the remaining data. Default below is the subgroup method.

Generating data sets

Consider this subset of the mtcars dataset:

dat0 <- mtcars[1:6,]
dat0
#>                    mpg cyl disp  hp drat   wt qsec vs am gear carb
#> Mazda RX4         21.0   6  160 110 3.90 2.62 16.5  0  1    4    4
#> Mazda RX4 Wag     21.0   6  160 110 3.90 2.88 17.0  0  1    4    4
#> Datsun 710        22.8   4  108  93 3.85 2.32 18.6  1  1    4    1
#> Hornet 4 Drive    21.4   6  258 110 3.08 3.21 19.4  1  0    3    1
#> Hornet Sportabout 18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
#> Valiant           18.1   6  225 105 2.76 3.46 20.2  1  0    3    1

Generate a list of data sets by resampling or by creating subgroups.

generate_data_list(dat0, K=3, method="subgroups")
#> [[1]]
#>                    mpg cyl disp  hp drat   wt qsec vs am gear carb
#> Mazda RX4         21.0   6  160 110 3.90 2.62 16.5  0  1    4    4
#> Datsun 710        22.8   4  108  93 3.85 2.32 18.6  1  1    4    1
#> Hornet Sportabout 18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
#> Valiant           18.1   6  225 105 2.76 3.46 20.2  1  0    3    1
#> 
#> [[2]]
#>                 mpg cyl disp  hp drat   wt qsec vs am gear carb
#> Mazda RX4 Wag  21.0   6  160 110 3.90 2.88 17.0  0  1    4    4
#> Datsun 710     22.8   4  108  93 3.85 2.32 18.6  1  1    4    1
#> Hornet 4 Drive 21.4   6  258 110 3.08 3.21 19.4  1  0    3    1
#> Valiant        18.1   6  225 105 2.76 3.46 20.2  1  0    3    1
#> 
#> [[3]]
#>                    mpg cyl disp  hp drat   wt qsec vs am gear carb
#> Mazda RX4         21.0   6  160 110 3.90 2.62 16.5  0  1    4    4
#> Mazda RX4 Wag     21.0   6  160 110 3.90 2.88 17.0  0  1    4    4
#> Hornet 4 Drive    21.4   6  258 110 3.08 3.21 19.4  1  0    3    1
#> Hornet Sportabout 18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
generate_data_list(dat0, K=3, method="resample")
#> [[1]]
#>                      mpg cyl disp  hp drat   wt qsec vs am gear carb
#> Mazda RX4           21.0   6  160 110 3.90 2.62 16.5  0  1    4    4
#> Hornet 4 Drive      21.4   6  258 110 3.08 3.21 19.4  1  0    3    1
#> Hornet Sportabout   18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
#> Hornet Sportabout.1 18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
#> Hornet Sportabout.2 18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
#> Valiant             18.1   6  225 105 2.76 3.46 20.2  1  0    3    1
#> 
#> [[2]]
#>                    mpg cyl disp  hp drat   wt qsec vs am gear carb
#> Mazda RX4 Wag     21.0   6  160 110 3.90 2.88 17.0  0  1    4    4
#> Datsun 710        22.8   4  108  93 3.85 2.32 18.6  1  1    4    1
#> Datsun 710.1      22.8   4  108  93 3.85 2.32 18.6  1  1    4    1
#> Hornet Sportabout 18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
#> Valiant           18.1   6  225 105 2.76 3.46 20.2  1  0    3    1
#> Valiant.1         18.1   6  225 105 2.76 3.46 20.2  1  0    3    1
#> 
#> [[3]]
#>                      mpg cyl disp  hp drat   wt qsec vs am gear carb
#> Mazda RX4 Wag       21.0   6  160 110 3.90 2.88 17.0  0  1    4    4
#> Hornet 4 Drive      21.4   6  258 110 3.08 3.21 19.4  1  0    3    1
#> Hornet 4 Drive.1    21.4   6  258 110 3.08 3.21 19.4  1  0    3    1
#> Hornet Sportabout   18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
#> Hornet Sportabout.1 18.7   8  360 175 3.15 3.44 17.0  0  0    3    2
#> Valiant             18.1   6  225 105 2.76 3.46 20.2  1  0    3    1

Model selection

Focus on entire dataset. For evaluation of the predictive ability of the selected model we set 20% of the data aside for validation. Hence we select models based on the remaining 80% of the data. Fit a linear model to each data set and select the best model by stepwise regression. This gives an indication of the stability of the model.

set.seed(1411)
dat <- personality
train <- sample(1:nrow(dat), 0.6*nrow(dat))
dat.training <- dat[train, ]
dat.testing <- dat[-train, ]

mod1 <- glm(agreebl ~ ., data = dat.training)

For each fold we can select models on the analysis part of the data set.

set.seed(1411)
n.searches <- 12
mod_stab <- model_stability_glm(dat.training, mod1,
                           n.searches=n.searches, method="subgroups", trace=0)
mod_stab
#> $rhs_matrix
#> 19 x 12 sparse Matrix of class "dgCMatrix"
#>                                
#> distant . . . 1 . . . . . . . .
#> carelss 1 1 1 1 1 1 1 1 1 1 1 1
#> hardwrk 1 1 1 1 1 . 1 . 1 1 . 1
#> tense   1 1 1 1 1 1 1 1 1 1 1 1
#> kind    1 1 1 1 1 . 1 . . . 1 1
#> relaxed 1 1 1 1 1 1 1 1 1 1 1 1
#> approvn 1 1 1 1 1 1 1 1 1 1 1 1
#> harsh   . 1 1 1 . . 1 1 1 . . .
#> persevr 1 1 1 1 1 1 1 1 1 1 1 1
#> friendl . 1 1 1 1 1 1 1 1 1 . 1
#> lazy    . . 1 1 1 . . 1 . . 1 .
#> coopera 1 1 1 1 1 1 1 1 1 1 1 1
#> quiet   . 1 1 1 1 1 1 1 1 1 1 1
#> withdrw . . . 1 . . . . . . . .
#> disorgn . . . . . 1 . . 1 . . .
#> respnsi . . . . . 1 1 1 1 1 . 1
#> contrar . . . . 1 1 . . . 1 . 1
#> worryin . . . . . . 1 1 1 1 . 1
#> sociabl . . . . . . . . . . 1 1
#> 
#> $freq
#>  [1] 1 1 1 1 1 1 1 1 1 1 1 1
summary(mod_stab)
#> $number_of_models
#> [1] 12
#> 
#> $number_of_unique_models
#> [1] 12
#> 
#> $number_of_predictors
#>  [1]  8 11 12 14 12 11 13 12 13 12 10 14
#> 
#> $frequency_of_predictors
#> distant carelss hardwrk   tense    kind relaxed approvn   harsh persevr friendl 
#>       1      12       9      12       8      12      12       6      12      10 
#>    lazy coopera   quiet withdrw disorgn respnsi contrar worryin sociabl 
#>       5      12      11       1       2       6       4       5       2

Specifically, the matrix shows the predictors selected in each model and below is the frequency with which each model is selected.

The outcome of the steps above is a list of models and as it is the same model selection method applied to each group of data, the difference (if any) in models is due to differences in the data in each group.

We can obtain fitted models as follows

formula(mod_stab, fit=FALSE) [1:2]
#> [[1]]
#> agreebl ~ carelss + hardwrk + tense + kind + relaxed + approvn + 
#>     persevr + coopera
#> <environment: 0x5a0ad84c9588>
#> 
#> [[2]]
#> agreebl ~ carelss + hardwrk + tense + kind + relaxed + approvn + 
#>     harsh + persevr + friendl + coopera + quiet
#> <environment: 0x5a0ad8539098>

This gives us a set of candidate models.

Predictive performance

We have selected a model based on subgroups of the training data. We can now evaluate the predictive performance of the selected model on the test data.

fit_list <- formula(mod_stab, fit=TRUE)

set.seed(1411)
cv.error <- cv_glm_fitlist(dat.training, fit_list, K=4)
cv.error
#>  [1] 1.03 1.13 1.04 1.23 1.10 1.10 0.95 1.01 1.01 1.08 1.16 1.13


cv3 <- sapply(fit_list, 
       function(fit) {
         x <- update(fit, data=dat.training)
         modelr::rmse(x, dat.testing)
       }
)
cv3
#>  [1] 1.26 1.29 1.30 1.30 1.36 1.36 1.31 1.35 1.36 1.38 1.23 1.36

plot(cv.error, cv3)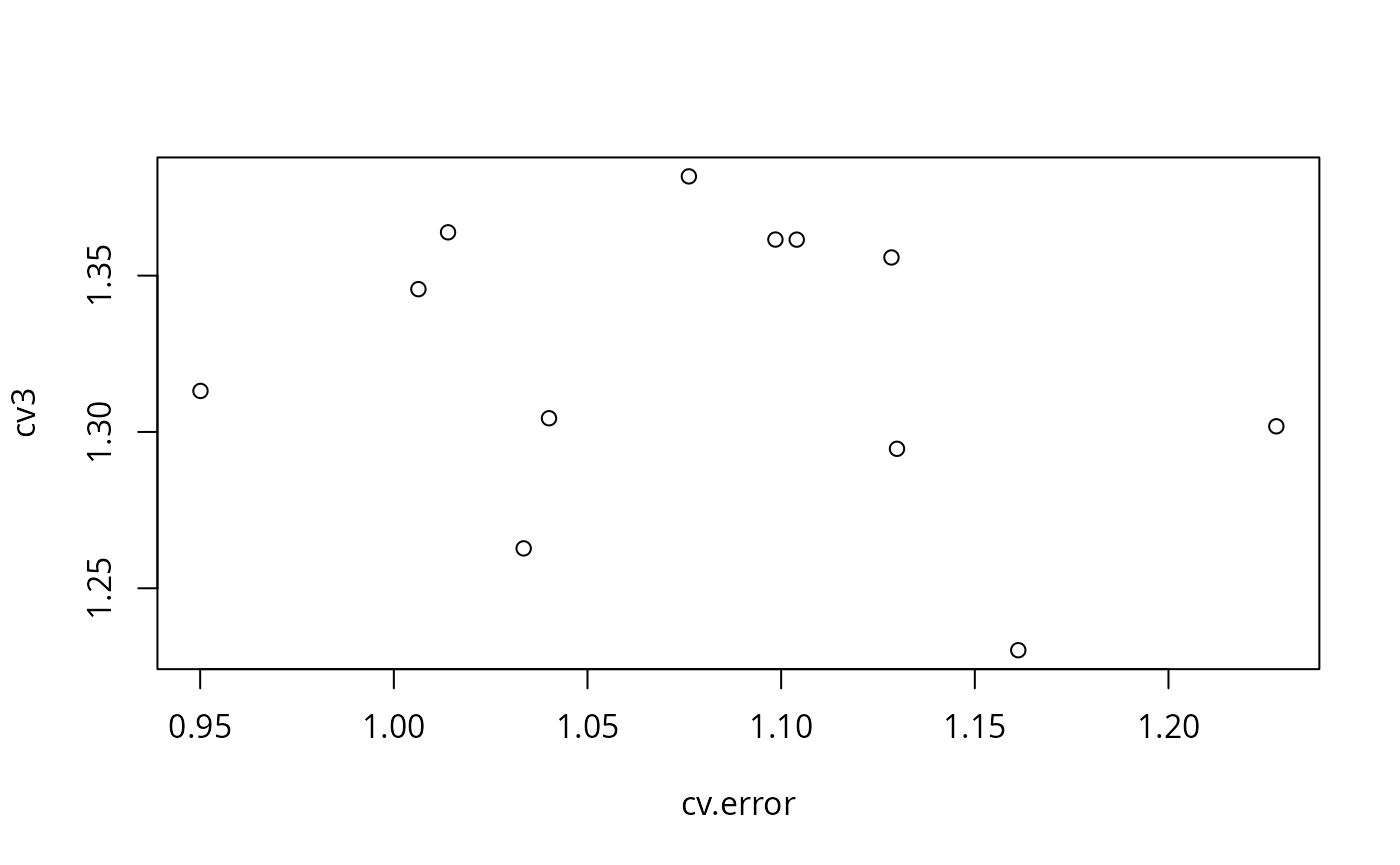

We can now evaluate the predictive performance of the selected model on the test data.

par(mfrow=c(1,2))
plot(sqrt(cv.error), main="Subgroups")
plot(cv3, main="Subgroups")

The plot on the left shows the cross validation error for the models selected in the subgroups. The plot on the right shows the prediction error for the models on the test data.

Søren Højsgaard